
이번 포스팅에서는 Khan academy의 linear independent(선형독립)에 대해 알아보자.
저번 학기에 다변량 수업을 들으면서, 벡터에 곱해지는 상수항들이 전부 0이면 선형독립이라는 걸 배웠(?)는데
그 의미에 대해 이해하지 못한채로 넘어갔었다. 살만 칸쌤 덕분에 드.디.어. 이해했다 ~!~!~!~!!!!
-
이게 영어로 이해하면 편한데, 한국어로 뭔가 어려운 단어를 써서 띠용스럽다.
나는 살만 칸쌤처럼 Linear Dependent / Independent 터미놀로지를 사용하겠다!!!!!!
Linear Independent전에 linear dependent를 먼저 이해해보자.
이전 포스팅에서 살펴보았듯, \(S = { \vec a, \vec b}\)일 때, \(Span(S)\)는 \(c_1\vec v_1 + c_2\vec v_2\)으로 나타낼 수 있는 모든 벡터의 집합이다.

예시로 이해해보자. Learn by example!
\(S = \{(2, 3), (4, 6)\}\)이라는 2차원의 벡터 2개로 이루어진 집합 S가 주어졌다.
\(Span( S ) = (c_1 + 2c_2)(2, 3)\)이다. (4, 6)은 (2, 3)의 두 배이기 때문! (집합의 한 벡터를 다른 벡터의 선형결합으로 나타내진다.)
즉, 두 벡터로 나타낼 수 있는 모든 벡터는 직선 위에만 있다는 것이다.
⇒즉, 집합 S는 Linear Dependent Set이다.
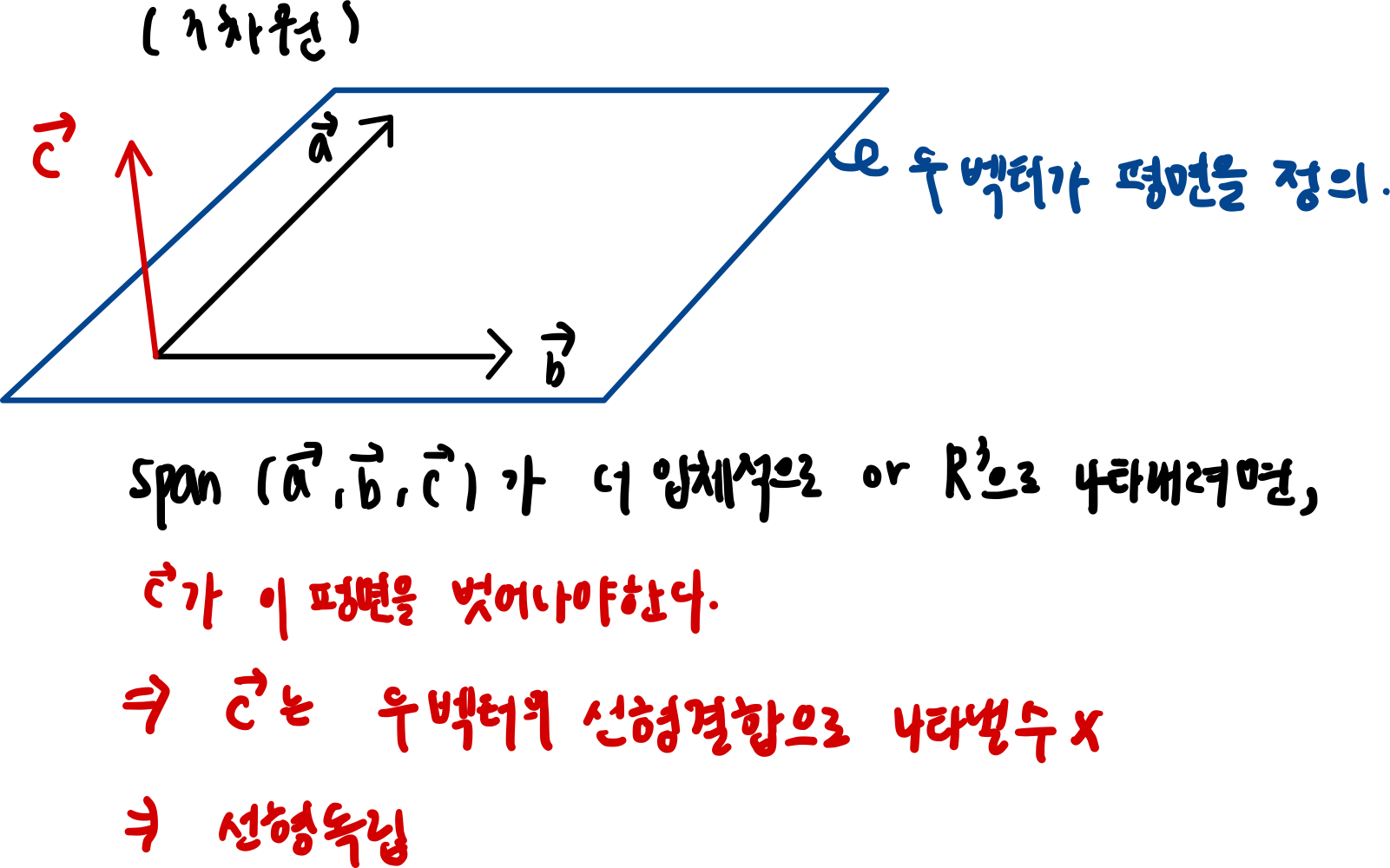
S가 Linear Independent하려면, 집합 S의 벡터들은 나머지 벡터들의 선형 결합으로 나타내지면 안된다.
쉽게 말해, S의 벡터들이 다른 방향을 가리켜야한다.
-
이번에는 예시가 아닌, 수학적 정의로 살펴보자.
\(S = \{ \vec v_1, \vec v_2, ... , \vec v_n \}\)가 있다.
해당 집합 S가 Linear Dependent set이면, 필요 충분 조건으로 \(c_1\vec v_1 + c_2\vec v_2 + ... + c_n\vec v_n = 0\)에서 모든 \(c_i\)들 중 적어도 하나이상은 0이 아니어야 한다.
이 정의를 증명하려면, 필요 조건과 충분 조건 모두가 성립하는지 살펴보아야한다.
i) 👉🏼 방향으로 증명
\(vec v_1 = a_1\vec v_2 + ... + a_n\vec v_n\)
⇔ \(0 = -\vec v_1 + a_2\vec v_2 + ... + a_n\vec v_n\)
즉,\(a_1=-1≠0\)이므로 조건이 참이다.
ii) 👈🏼방향으로 증명
\(c_1 ≠ 0\)이라고 가정하자.
\(c_1\vec v_1 + c_2\vec v_2 + ... + c_n\vec v_n = 0\)
⇔ \(\vec v_1 + \frac{c_2}{c_1}\vec v_2 + ... + \frac{c_n}{c_1}\vec v_n = 0\)
∴\(\vec v_1 = \frac{c_2}{c_1}\vec v_2- ... -\frac{c_n}{c_1}\vec v_n\)로 나타낼 수 있다.
즉, \(\vec v_1)\를 다른 벡터의 결합으로 표현할 수 있으며, 해당 벡터들을 포함하는 집합은 linear dependent set이 된다.
-
다음은 Linear Dependent / Independent의 다양한 예시들이다.
EX1)
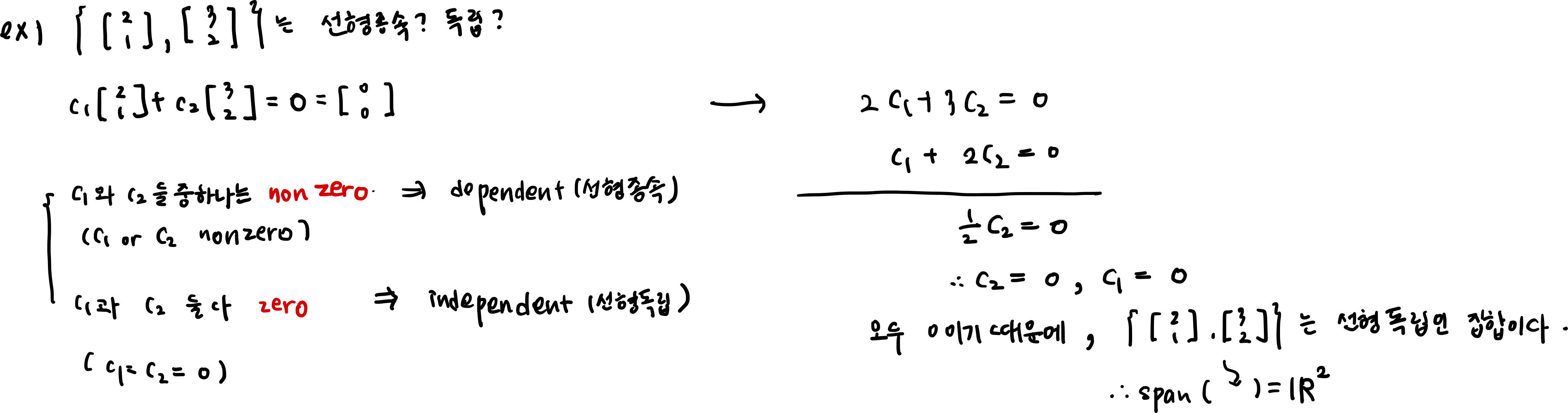
EX2)

즉, a=b=c=0이기때문에, linear dependent하지 않고 linear independent하다.
선형 독립은 해당 집합의 모든 벡터들이 다른 방향을 나타낸다는 것이다 ! ! !


