node2vec: Scalable feature learning for networks

논문 리뷰를 해보고자 함. graph를 알아보고자..

[논문 해석]

 

section 1. introduction

1. 네트워크 분석에서 많은 task들은 nodes와 edges에 대한 예측을 포함. 일반적인 node 분류 작업에서, 우리는 네트워크에서 node에의 가장 가능성있는 레이블을 배정하고자 함.  (ex. 소셜네트워크에서, 사용자의 흥미 예측에 관심) link 예측에서, 우리는 네트워크의 한 쌍의 노드가 그들을 연결하는 edge로 연결되는지를 예측하고자함. 다양한 도메인에 활용됨. 유전학에서는 유전자들 간 새로운 상호작용발견, 소셜네트워크에서는 실제 친구를 식별.

--> 네트워크분석: a pair of nodes가 edge로 connect되어있는지 여부를 판단하고자 함.

2. 모든 supervised 머신러닝 알고리즘은, 유익하고 차별성있고 독립적인 feature들을 필요로함. 네트워크의 예측문제에서는, 이것은 nodes와 edges에 대한 feature 벡터 표현을 구성해야함을 의미. 전형적인 솔루션은 전문가 지식에 기반하여 손수 domain-specific features를 포함하는 것. feature 엔지니어링에 필요한 노력들을 줄인다하더라도, 그렇게 생성된 feature들은 어떠한 특수한 task에만 사용가능하고, 일반화 되지가 않는다는 단점.

--> feature vector representation 필요. 이때, feature engineering에 많은 노력이 필요.

3. 대안: optimization문제를 해결함으로써 feature representation을 학습하는 것. 피쳐학습에의 챌린지는 목적함수(objective function)을 정의하는 것이다. (계산효율성과 예측 정확도의 밸런스를 맞추는) 스펙트럼의 한쪽면에서는, 다운스트림 예측작업의 성능을 최적화하는 feature representation을 직접 찾을 수 있음. 반면, 좋은 성능은, 예측해야하는 파라미터 개수를 증가시키므로, 높은 트레이닝 시간 복잡도를 초래. 다른 극단에서는, 목적함수는 다운스트림 예측 과제와 독립적으로 정의될수 있고, 이 representations는 순전히 unsupervised방식으로 학습될 수 있다. 이것은 최적화 계산을 효율적으로 만들고, 신중한 설계목적을 통해, task-독립적인 feautres들을 낸다. 

4. 그러나 현재기술은 만족스럽게 정의하고, (네트워크에서 확장가능한 unsupervised feature 학습을 하는)합리적인 목적함수를 최적화하는데에 실패. 선형, 비선형 차원축소(PCA), 다차원 스케일링과 확장 등의 고전적인 방법들은 data representation의 변동을 최대화 하기 위해, 네트워크의 대표적인 data matrix를 변환하는 목적함수를 최적화. 결과적으로, 이런 방법들은 가변적으로, 대규모 리얼월드 네트워크에서 값비싼 적절한 data matrix의 고유값 분해를 필요로 함. 더 나아가서, 잠재적 표현 결과는 network를 통한 다양한 예측과제에 대한 나쁜 성능을 보임.

--> classic한 방법들은 성능 bad.

 

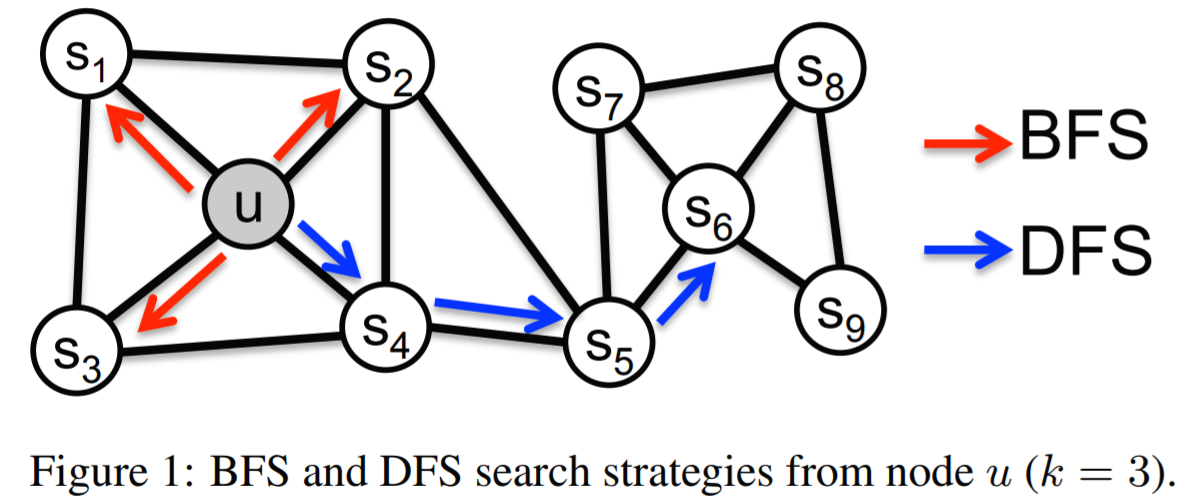
5. 대안적으로, nodes의 지역적인 이웃의 보존을 탐색하는 목적함수를 설계할 수 있음. 이 목적함수는 SGD를 활용해서 효율적으로 최적화할 수 있음. 이러한 방향에의 최근의 시도들은 효율적 알고리즘을 제안했지만, 네트워크 이웃의 경직된 개념에 근거하고있음. 이로인해서, 이 접근 방법들이 네트워크 고유의 연결 패턴에 둔감해지게 됨. 특히, 네트워크의 노드는 그 노드들이 속한 communities에 기반하여 구성된다.(homophily). 다르게는, 이 구성은 네트워크에서 노드들의 구조적 역할에 기반한다(structural equivalence) 예를들어, 그림 1에서, 노드 u와 s1를 관측. u와 s1은 같은 커뮤니티에 속함. 반면, u와 s6은 다른 구역의 커뮤니티에 있지만, hub node로써의 구조적 역할을 함. 리얼월드 네트워크는 공통적으로 이러한 equivalence의 혼합을 나타냄. 따라서 두가리 원리(1. 같은 네트워크 커뮤니티의 노드들을 가까이 embed 2. 비슷한 역할을 공유하는 node가 비슷한 embedding을 갖도록.)를 모두 준수하는 node representations를 학습하ㅡㄴ 유연한 알고리즘이 필요함.  이렇게 하면, feature학습 알고리즘은 다양한 도메인과 예측 수행에서 일반화가 가능해질 것임.

--> homophily와 structural equivalence를 동시에 만족하는 유연한 feature learning알고리즘을 사용하자.

6. present work. node2vec제안. 이것은 네트워크에서 확장가능한 feature 학습을 위한 semi-supervised알고리즘. 자연어처리에서의 이전 작업에서 motivate된 SGD를 사용하여 사용자정의 그래프기반 목적함수를 최적화함. 직관적으로, 우리의 접근은 d차원 feature 공간에서, nodes의 네트워크 이웃들을 보존하는 가능성(우도)을 극대화하는 feautre representation을 반환할 것임. 우리는 2차 랜덤워크 접근방식을 사용하여, 노드의 네트워크 환경을 생성한다.

7. key contribution은node의네트워크이웃의 유연한 개념을 정의하는것.적절한 개념을 고름으로써, node2vec은 노드들이 속하는 커뮤니티나 네트워크의 역할에기반하여 nodes를 구성하는 representation을 학습.  효율적으로 다양한 이웃을탐ㅅ색하는 biased 랜덤워크의 family를 개발함으로써 이 방법을 성취. 이 알고리즘은 유연하고, 조정가능한 파라미터를 통해 탐색 공가을 제어할 수 있게함. 결과적으로, 이 방법은 이전 작업을 일반화하고, 네트워크에서 관찰된 동등성의 전체 스펙트럼을 모델링할 수 있음. 직관적인해석을 갖고있고, 다른 네트워크 탐색 전략에 대한 walk를 편향시킴. 이 파라미터들은 semi-supervised방식으로 레이블된 데이터의 아주 작은 비율을 가지고 직접 학습될 수 있음. 

8. 개별 노드들의 feature 표현이 어떻게 nodes의 쌍으로 확장되는지 보여줌. edges의 feature 표현을 생성하기 위해, 우리는 심플한 이항연산자로 개별 노드의 표현 학습을 구성한다. 이 합성성은 node2vec이 예측 작업에 nodes뿐만아니라 edges까지 할 수 있게 함.

--> learning feature reperesentations of nodes를 binary operator로 

9. 우리 실험은 네트워크에서 두개의 공통적인네트워크의 예측 작업에 초점. 1. multi-label 분류작업(모든 노드가 하나이상의 클래스 레이블에 배정된) 2. link 예측작업(nodes의 쌍이 주어졌을때, edge긔 존재 유무를 예측하는). 본 논문에서는 node2vec과 SOTA 알고리즘의 성능을 대조. 우리는 다양한 도메인의 리얼월드 네트워크로 실험함.(소셜네트워크, 정보 네트워크, 샐물학 네트워크) 실험은 node2vec이 sota 방법보다 멀티레이블분류에서는 최대 26.7%, 링크예측에서는 12.6%까지 성능을 능가. 이 알고리즘은 10% 레이블된 데이터만으로 경쟁적인 성능을 보여주며, noise가 있거나 edge가 누락된 형태에서도 robust하다. 계산적으로, node2vec의 주요 단계는 병렬화가능. 몇시간안에 수백만개의 노드를 가진 네트워크로 확장할 수 있음.

--> 작업 1. multi-label 분류 2. link 예측 / sota알고리즘보다 성능 뛰어남. / (+) robust, 확장성up

10. process.

• SGD를 이용하여, 새로운 네트워크인식하고  이웃보존하는 목적함수를 효율적인 최적화하는 네트워크에서의 feature learning 을 위한  알고리즘 node2vec제안.

• node2vec이 network science의 확립된 원칙에 따라 어떻게 부합하는지 보여주고, 서로 다른 동등성에 부합하는representations를 발견하는 데에 유연성을 제공함.

• node2vec 및 기타 feature learning methods를 확장. edge기반 예측 문제에서 nodes에서 노드의 쌍까지 이웃보전하는 목적함수를 기반으로. 

• 경험적으로 node2vec을 평가 (다중분류와 링크예측. 실제 데이터셋에서)

section 2. Related Work

1. feature engineering은 머신러닝에서 광범휘하게 연구됨. 네트워크에서는, 노드에 대한 feature를 생성하는 전통적인 패러다임은 (일반적으로 네트워크 속성에 기반해서 수공예적인 features를 포함하는) feature추출 기술에 기반. 대조적으로 우리의 목표는 "feature추출을 representation 학습문제로 캐스팅함으로써, 전체 과정을 자동화하는 것." 더이상 수작업 설계는 필요없어질 것.

2. unsupervised feature 학습은 그래프의 다양한 행렬표현(특히, 라플라시안, 인접행렬)의 스펙트럼 속성을 이용. 선형대수관점에서, 이 방법들은 차원축소로 볼 수 있음. PCA와 같은 선형과 비선형(IsoMap) 차원축소기술이 제안되어옴. but 이런 방법들은 계산적, 통계적성능의 결함 단점. 계산효율성 관점에서, 솔루션 품질이 근사치로 현저히 저하되지않는 한 데이터 매트릭스의 고유값분해(eigendecomposition)는 매우 비싼 연산임. 따라서 이 방법(차원축소)은 큰 네트워크로 확장시키기 어려움. 그리고, 네트워크에서 관찰되는 다양한 패턴들에 robust하지 못하는 목적함수에 최적화하고, 네트워크 구조와 예측과제의 관계에 대해 가정함. 예를들어, spectral clustering은 그래프 cuts가 분류에 유용할 것이라는 강한 homophily 가정을 만듦. 이러한 가정은 많은 시나리오에서 합리적이지만, 다양한 네트워크에 거쳐서는 효과적으로 일반화하기 어려움.

--> 그래프의 다양한 행렬표현 / 차원축소: 1. 비싼 연산 -> not scalable 2. robust하지못함

 3. 자연어처리의 representation 학습에의 최근 발전은 단어와 같은 이산적인 객체들의 feature 학습에의 새로운 길을 열었음. 특히, Skip-gram 모델은 likelihood 목적을 보존하기위해, neigborhood를 최적화함으로써  단어의 연속적인 feature 표현을 학습하는 것이 목표.알고리즘 진행: 문서의 모든 단어들을 스캔 -> 모든 단어에 대해, 단어들의 features는 근처의 단어들을 예측할 수 있도록 그것을 포함하는 것을 목표로함. 단어 feature representations는 negative sampling으로 SGD를 활용하여 likelihood 목적함수를 최적화함으로써 학습. Skip-gram의 목표는 유사한 맥락의 단어들이 유사한 의미를 갖는 경향이 있다는 것을 가정. 즉, 비슷한 단어의 neighbor에서 비슷한 단어가 나타나는 경향. 

4. skip gram연구에서 영감을 받아, 최근 연구는 네트워크를 "문서"로 표현함으로써 네트워크의 유추를 확립. 문서와 비슷한 방법은 순서가 정해진 단어들의 시퀀스인데, 네트워크로부터 노드 순서를 샘플링하여 네트워크를 순서가 정해진 노드로 바꿀 수 있음. 그러나 노드에 대해 가능한 샘플링 전략이 많아서, 학습된 feature representation마다 다른 결과를 보여줌. 사실, 우리가 보여주어야할 것 처럼, 모든 예측, 분류 문제에서 명확하게 잘되는 것은 없음. 이는 네트워크 노드 샘플링에 유연성을 제공하지못하는 prior work의 단점. 우리의 알고리즘 node2vec은 특정 샘플링 전략에 묶이지않고, 탐색하는 서치공간을 조절하게하는 파라미터를 제공함으로써, 이러한 한계를 극복.

5. -

section 3. Feature Learning framework

1. 네트워크에서의 feature학습을 최대우도 최적화 문제로 공식화한다. 주어진 네트워크를 G=(V, E)로 표현. 우리의 분석은 일반적이고, 모든 (비)방향, (비)가중치 네트워크에도 적용됨. 함수 f: V -> d차원. 함수 f를 매핑 함수(다운스트림 예측 작업에 대해 학습하고자하는 nodes -> feature representations). d: 파라미터(feature representations 차수). 똑같이, f는 크기 |V| x d매개변수의 행렬. 모든 소스 노드 u ∈ V에 대해, N_S(u) ⊂ V를 정의. 이때, N_S(u)는 이웃 샘플링 전략 S를 통해 생성된 노드 u의 네트워크 인접 이웃을 나타냄.

2. skip-gram 아키텍처를 네트워크로 확장.  f가 주어졌을때, feature representations를 조건화한 노드u에 대해 네트워크 인접 이웃을 관측하는N_s(u)의 로그-확률을 최대화하는 목적함수를 최적화하고자함. 식:: 

 

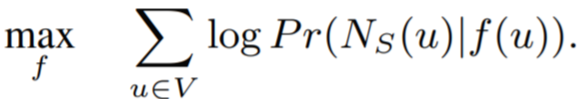
3. 최적화문제를 다루기쉽게하기위해, 두가지 standard 가정을 세운다. 

• 조건부 독립: 노드u가 주어졌을 때, 다른 이웃 노드들이 관측될 확률은 모두 독립적.

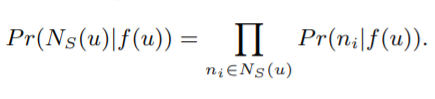
• feature space에서 대칭: source 노드와 인접 노드는 feature space에서 서로 대칭적인 영향미침. 따라서, 우리는 모든 소스-이웃 노드의 쌍의 조건부 likelihood를 softmax로 모델링.

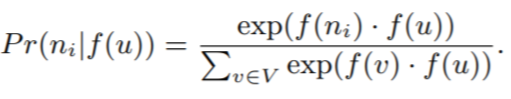
4. 위의 두가지 가정으로 인해, 목적함수 max~가 간소화됨. 

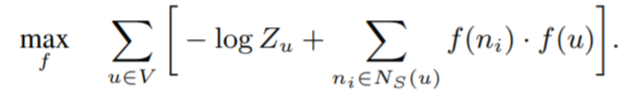
5. skip-gram은 원래 NLP영역에서 개발됨. 텍스트의 선형성을 고려할때, 이웃의 개념은 원래 연속된 단어에 대해 슬라이딩 창을 이용하여 정의됨. 그러나 네트워크는 리니어하지않고, 따라서 이웃에 대한 더 풍부한 개념이 필요! 이 문제를 풀기위해, 우리는 주어진 소스 node u의 많은다른 이웃들을 추출하는 랜덤화된 절차를 제안. 이웃 N_S(u)는 단지 가까운 이웃에만 제한되지않고, 샘플링전략S에 따라 다른 구조를 가질 수 있음.

 

section 3.1: Classic search strategies

1. 소스 노드의 이웃을 샘플링하는 문제를 loacl search의 한 형태로 본다. 그림1을 보자.  소스노드 u가 주어졌을 때, 우리의 목표는 이웃노드 N_S(u)를 생성/샘플링하는 것. 중요한 것은, 다른 샘플링전략 S를 공정하게 비교할 수 있도록, 이웃집합인 N_S의 크기를 k nodes로 제한. 그리고 싱글 노드u에 대해 여러세트를 샘플링. 일반적으로, 두개의 극단적 샘플링 방법이 존재.

• BFS(Breadth-first Sampling)-너비우선탐색
  N_S를 소스 노드의 직접적인 이웃에 제한.  그림1에서 N_S(u) = {s1, s2, s3} , k=3

• DFS(Depth-first Sampling)-깊이우선탐색
  소스 노드에서 점점 먼거리에서 순차적으로 샘플링되는 노드들로 구성. 그림1에서 N_S(u) = {s4, s5, s6}, k=3

 

2. 너비우선,깊이우선 샘플링은 다른 시나리오. 학습된 repersentatios에 대한 관심을 갖는 영향, 암시, 함축으로 이어지는 탐색공간의 관점에서. 

3. 특히, 네트워크의 노드에 대한 예측 작업은 두 종류의 유사성 사이를 왕복한다.(왔다갔다한다). homophily, structural equivalence. homophily 가정하에서, 강하게 연결되어있고 비슷한 네트워크 클러스터에 속해있는 노드들은 매우 가깝게 임배딩되어야 함. ex) s1, u
반대로, structural equivalence 가정하에서는, 노드들이 네트워크에서 비슷한 구조를 가질때, 비슷한 공간에 임배딩됨. ex) u, s6 - 각 network community의 hub역할을 함. 중요한 것은 연결성을 강조하지않음. 즉, 노드는 네트워크에서 멀리 떨어져있을수있지만, 여전히 동일한 구조적 역할은 가질 수 있음. 

리얼 월드에서는, 이러한 동등성 개념은 배타적이지않음. 네트워크들은 일반적으로 일부 노드가 homophily를 보이는 반면, 다른 노드는 구조적 동등성을 반영하는 두 가지 동작을 나타냄.

4. BFS와 DFS 전략이 위의 동등성 중 하나를 반영하는 representations를 만드는 데 핵심적인 역할. 특히, BFS로 샘플링된 이웃들은 구조적 동등성에 가까운 임베딩. 직관적으로, 구조적 동등성을 확인하려면, local한 이웃들의 특성을 정확히 파악하는 것으로 충분함. 예를들어, 교량역할과 허브역할과 같은 네트워크 역할에 기반한 구조적 동등성 각 노드의 직접적인 이웃을 관찰하는 것만으로도 추론됨. 가까운 노드의 탐색을 제한함으로써, BFS는 이러한 특성들을 달성하고, 모든 노드의 이웃에 대한 미시적인 관점을 얻음. 또한 BFS에서는 샘플링된 이웃들은 여러번 반복되는 경향이 있음. 소스 node에 대한 1-hop 노드 분포 특성화의 분산을 감소시키므로 이 또한 중요하다. 그러나 그래프의 매우 작은 부분은 주어진 k에 대해 탐색됨.

--> BFS는 network의 미시적인 특성을 강조. (homophily) / DFS는 거시적특성 강조. (structural equivalence): 비슷한 노드는 서로 비슷한 구조적 위치 --> 노드들의 직접적 이웃을 관찰하는것으로 추론 가능)

5. 소스 노드u로부터 더 멀리 이동할 수 있기때문에(샘플 사이즈가 k로 고정된 상태에서), 네트워크의 거시적인 부분을 탐색할 수 있는 DFS. DFS로 샘플링된 노드는 homophily에 기반한 커뮤니티를 추론하는데에 필수적인 이웃의 거시적 시각 정확하게 반영. 그러나, DFS의 문제는 네트워크에 존재하는 노드 대 노드 의존성을 유추하는 것뿐만 아니라, 이러한 종속성의 정확한 성격을 특징짓는 것이 중요하다는 것. 샘플링하는 사이즈 k에 제약을 갖고있고, 탐색할 수 있는 이웃의 크기가 크기때문에, 분산이 높아짐. 그리고, 샘플링된 노드가 소스와 멀리 떨어져 있고 잠재적으로 덜 대표적일 수 있기 때문에, 훨씬 더 깊은 곳으로 이동하면 복잡한 종속성의 문제로 이어짐.

--> DFS는 분산이 높고, 복잡한 종속성의 문제가 있음.

section 3.2: node2vec

3.1 섹션의 관찰을 바탕으로, 우리는 BFS와 DFS를 원활하게 보충하게 하는 유연한 이웃 샘플링 전략을 설계함.

3.2.1 Random walks

소스노드 u가 주어지면, 고정된 길이 l에 대한 랜덤워크를 시뮬레이션한다. c_iㄹ르 walk에서 i번째 노드라고 하자(c0=u부터 시작). 노드 c_i는 이러한 분포에 의해 생성됨. 

 

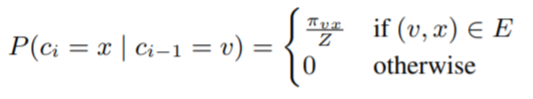
π_vs: 노드v와 노드x간의 비정규화된 transition probability(전이확률: state가 v에서 x로 이동할 확률), Z는 정규화 상수(사후확률을 적분했을때 1이 되도록 만들어주는 역할. [참고])

3.2.2 Search bias α

랜덤워크를 편향시키는 가장 간단한 방법은 정적 엣지 가중치 w_vx를 기반으로 다음 노드를 샘플링하는 것. 그러나 이것은 네트워크 구조를 설명할 수 없고, 다른 유형의 네트워크 이웃을 탐색하는 탐색 절차를 안내함. 추가적으로, BFS와 DFS와는 다르게, 랜덤워크는 동등성의 개념이 경쟁적이지않고 둘의 혼합됨을 보여줌. 

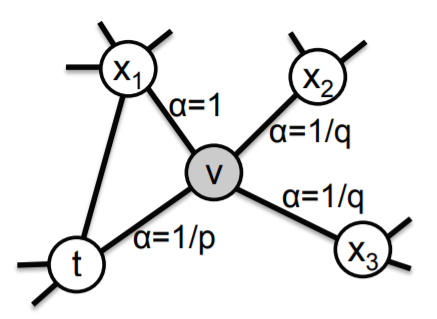
2차 랜덤워크를 정의. 그림2에서 보면, 파라미터는 p와 q. 방금 edge(t,v)를 가로지르고 현재 노트v에 있는 랜덤워크를 고려. walk는 다음에 어디로 갈지를 결정해야한다. 따라서 v로부터 이어지는 엣지(v,s)에 대한 전이확률 π_vs를 평가해야함. 이때 우리는 π_vs를 비정규화된 전이확률로 설정을 했음. π_vs = α_pq(t,x)*w_vs.

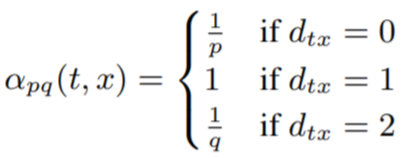
d_tx: 노드t와 x간의 최단경로. d_tx는 {0,1,2}중 하나의 값을 갖고, 따라서 walk를 안내하기위해 두 개의 파라미터가 필요함.  

직관적으로 파라미터 p와 q는 얼마나 빠르게 walk가 주변을 탐색하고, 이웃에서  나가는 속도를 제어함. 특히 파라미터는 검색 절차를 BFS와 DFS 사이에 (대략) 보간할 수 있도록 하며, 따라서 노드 동등성에 대한 서로 다른 개념에 대한 관련성을 반영함.

return parameter, p.
파라미터 p는 walk에서 즉시 재방문하는 노드의 likelihood를 제어함. p를 높게 설정하는 것은 다음 두 단계에서 이미 방문한 노드를 샘플링할 가능성이 낮춤. 이 전략은 중간 수준의 탐색을 장려하고 샘플링 시 2-hop 중복성을 방지함. 반면 p가 낮으면(<min(q, 1)), 한 단계 뒤로 walk를 이끌고, 시작 노드에서 walk를 가깝게 유지한다. 

--> return parameter p가 높으면, 새로운 노드로 가는 경향 / 낮으면, 시작노드에서 walk를 가깝게 유지

In-out parameter, q.
파라미터 q는 탐색이 안쪽으로 향하는 노드와 바깥으로 향하는 노드 간의 구별을 가능하게 함. 그림 2에서 보면, q>1일때, 랜덤 워크는 노트 t에 치우쳐져있음. 시작 노드에 대한 기본 그래프의 지역적인 관점을 얻고, 작은 지역내에서 노드로 구성되므로 BFS와 비슷함. 
반대로, q<1이면, 노드가 노드t로부터 멀리떨어진 노드를 방문하는 경향이 있음. 이것은 밖으로 향하는 탐색을 장려하는 DFS과 비슷. 그러나 본질적인 차이점은 우리가 랜덤워크 프레임워크 내에서  DFS와 비슷한 탐색을 이루는 것이다. 따라서, 샘플링된 노드들은 주어진 소스노드 u로부터 거리를 엄격하게 늘리는 것이 아니고, 랜덤워크의 우수한 샘플링 효율성과 다루기쉬운 전처리의 이점을 누린다. 워크t에서, π_vs 를 선행 노드의 함수로 설정함으로써, 랜덤 워크는 2차 markovian(마코비안). (??)

--> in-out parameter q가 1보다 크면, BFS과 비슷. locality / 1보다 작으면, DFS와 비슷. 

benefits of random walks.
순수한 BFS/DFS에 비해 이점 여러가지. 랜덤 워크는 공간적 시간적 효율성O. 그래프의 모든 노드의 직접적인 이웃들을 저장하는 공간복잡도는 O(|E|). 2차 순서 랜덤워크의 경우네는, 모든 노드의 이웃들 간의 상호연결을 저장하는 것이 좋음. 이 때는, 공간 복잡도가 O(a^2|V|). a는 그래프의 평균 degree이고, 이것은 보통 실제 네트워크에서는 작은 값. 
클래식 탐색 기반 샘플링 전략에 비해 랜덤 워크의 또 다른 이점은 시간 복잡도. 특히, 샘플 생성 과정에서 그래프 연결을 부과함으로써, 랜덤 워크는 편리한 매커니즘을 제공. 다른 소스 노드들을 거쳐서, 샘플들을 재사용함으로써 샘플링 속도를 효과적으로 높임. 길이 l(>k)의 랜덤워크를 시뮬레이션 함으로써,  랜덤 워크의 마르코반 특성덕에 l-k개의 노드에 대한 ㅏk개의 샘플들을 한번에 생성. 따라서 효율적인 복잡도는 샘플 당 O(1 / k(l-k) )이다. 

예를 들어, 그림 1에서 랜덤워크 {u, s4, s5, s6, s8, s9}의 길이 l = 6을 샘플링하여 N_S(u) = {s4, s5, s6, s8}, N_S(s5) = {s6, s8} 및 N_S(s5) = {s6, s8, s9}을 샘플링. 샘플 재사용은 전체 절차에 약간의 bias생길 수 있음. 대신 성능이 매우 좋아짐.

 

3.2.3 The node2vec algorithm

pseudocode for node2vec

랜덤워크에서, 출발 노드 u의 선택으로 인한 암묵적인 vias가 있었음. 우리는 모든 노드에 대한 representations를 학습하기 떄문에, 이 bias를 상쇄한다. 모든 노드로부터 시작하는 고절 길이 l의 r랜덤워크를 시뮬레이션함으로써. walk의 모든 스템마다, 샘플링은 전이 확률 π_vs에 기반해서 이뤄짐. π_vs는사전계산이가능하므로,노드의 샘플링이 O(1)시간내에 효율적으로 수행됨. node2vec의 세가지 단계: 1. 전이확률을 계산하는 전처리 2.랜덤워크 시뮬레이션 3. SGD를 이용한 최적화. 순차적으로 수행됨. 각자 단계는 비동기적으로 병렬처리 및 실행되어 node2vec의 전체 확장성에 기여.

 

[리뷰]

 

   참고 블로그1: frhyme.github.io/machine-learning/node2vec/ 

node2vec은 무엇인가?

참고 블로그2: analysisbugs.tistory.com/m/214

[논문 리뷰] node2vec: Scalable feature learning for networks

참고 블로그3: medium.com/@harry_41860/%EA%B7%B8%EB%9E%98%ED%94%84-%EC%9E%84%EB%B2%A0%EB%94%A9-%EC%9A%94%EC%95%BD-a0a34527bb3f 

그래프 임베딩 요약